This video explains percentages in a simple way, showing how they’re basically just fractions or decimals. It covers stuff like getting 10% of a number by multiplying by 0.1, adding 10% by using 1.1, or subtracting by 0.9. Learning how to calculate percentages using decimals and fractions, is often easier, faster and can be done in one’s head—without the use of a calculator.
percentage as fractions
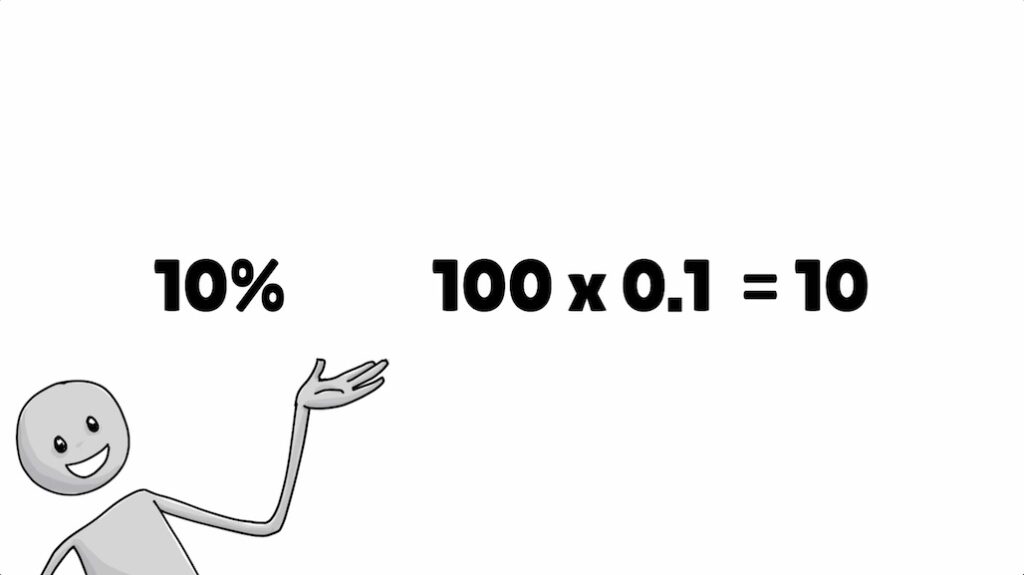
To find 10% of something, multiply by 0.1. To add 10% to something, multiply by 1.1. To deduct 10% from something, multiply by 0.9. And if you want to find out what’s 70% of 20, all you need to do is eliminate and multiply. In this video, you’ll learn why when you see percentages, you should think of fractions.
What is percent?
The word “percent” comes from Latin and means “per hundred”. If you have a basket with 100 apples and take out the 7 rotten ones, that’s 7 per hundred. And if you instead want to estimate the rotten ones out of 300 apples, multiply 7 by 3—which is 21.
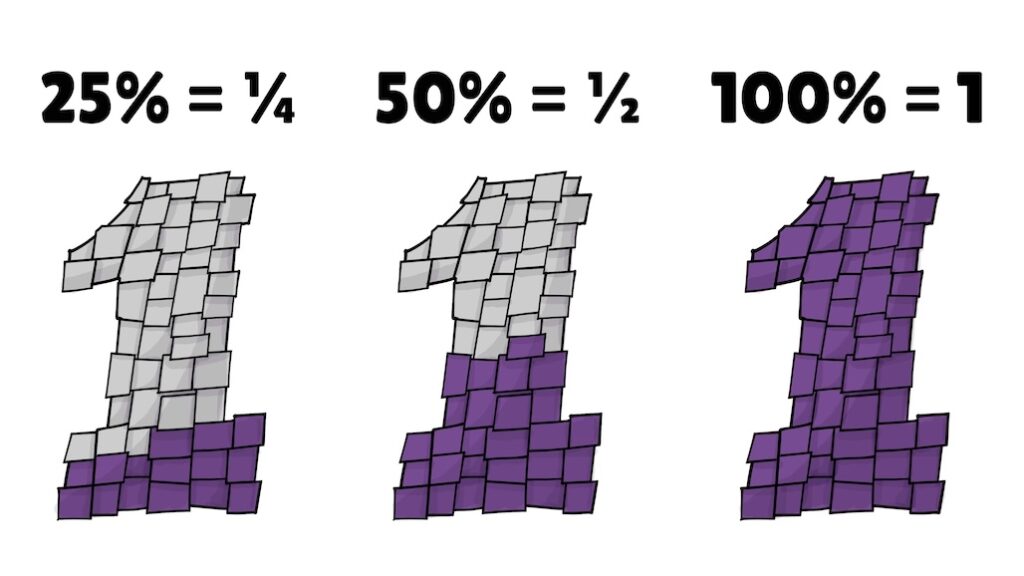
Understanding percentages as “part of 100” is good. Even better is seeing percentages as a fraction of 1—like part of one pile or a slice of a whole pizza. That’s because, 25% is a 1/4 of 1. 50% is 1/2 of 1. 100% is 1.
history of %
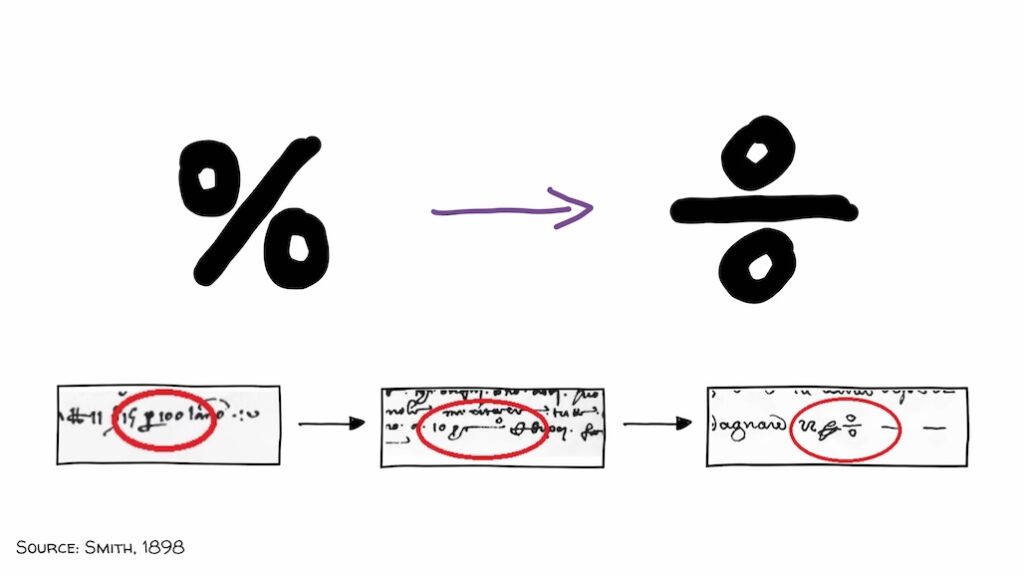
Italians understood this centuries ago. They didn’t have the % symbol yet. Instead, they used a flipped version of it, which evolved from writing “per cento” and looked a lot like a division sign. Which made sense.
When you see, for instance, 25%, picture part over whole. Which is equivalent to 1/4, or 0.25. The decimal is what we are really after.
hotel example
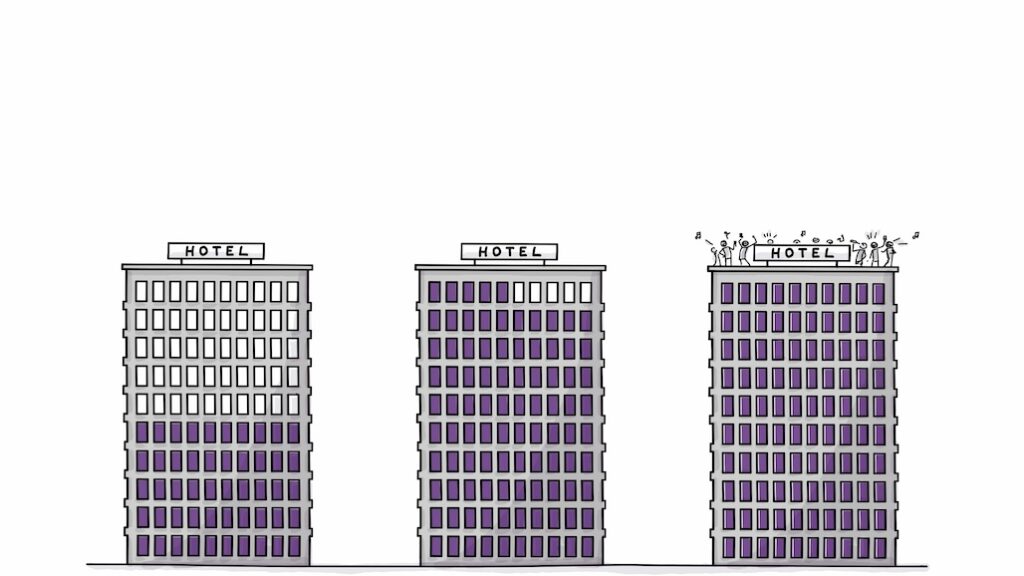
Imagine you own a hotel with 100 rooms. In the low season, 50% of rooms are booked. In the high season, 95% are full. On New Year’s Eve, all 100 rooms are reserved!
adding percentages
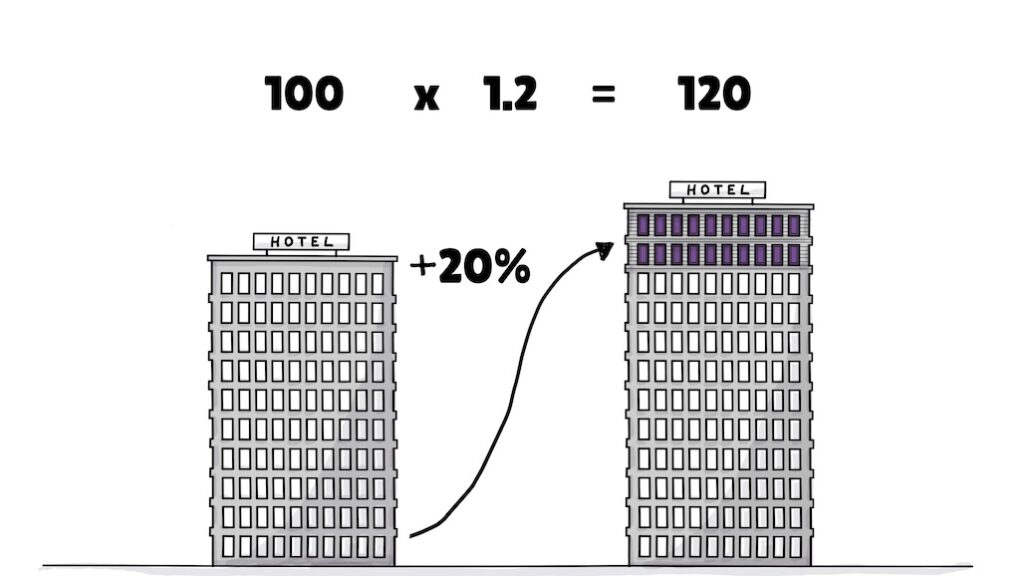
Now business is booming and you want to increase capacity by 20%. Using decimals makes this easy. This is because 1, plus .2 of that one is 1.2. Again: 1 plus point 2 is 1.2. To add 20% to something, you take your whole, multiply it by 1.2 and solve your equation. Which, in this case, gives you 20 rooms on top.
Now say, you want to expand again, this time by 25%. So you take your 120 rooms and multiply them by 1.25, to add the part you want to increase it by. The result is 150 or 30 rooms on top of your whole.
reducing percentages
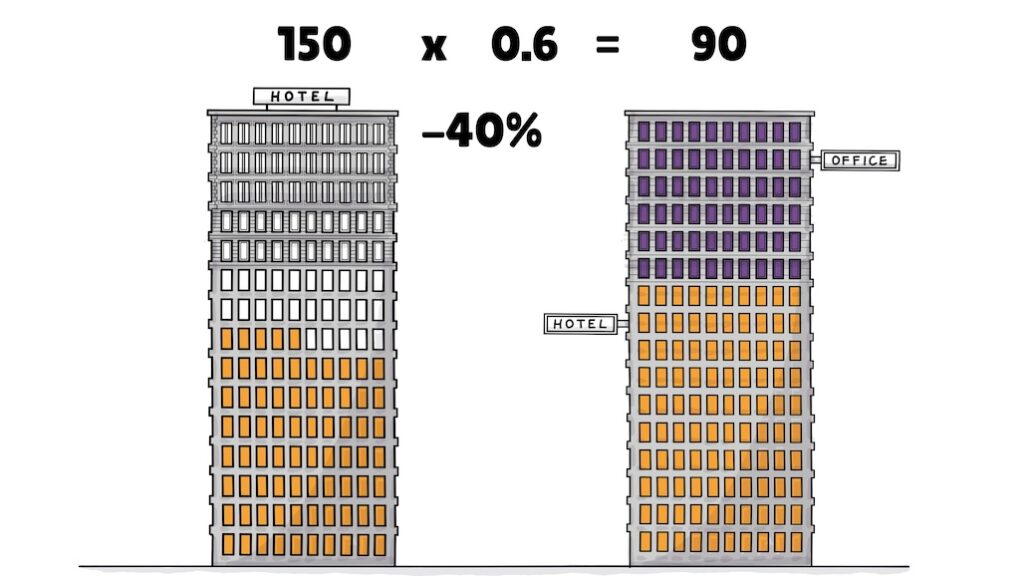
Now, say there is a crisis, only half of your hotel is booked, and you want to downsize by 40%. This works in exactly the same way. You take your whole and deduct point 4, which gives you the figure you use to multiply your whole with.
Or put differently, to deduct 40%, you take the whole, multiply it by .6, and solve your equation. Which in this case leaves you with 90 rooms for your hotel and 60 you could turn into an office. That’s really all there is to it!
conclusion
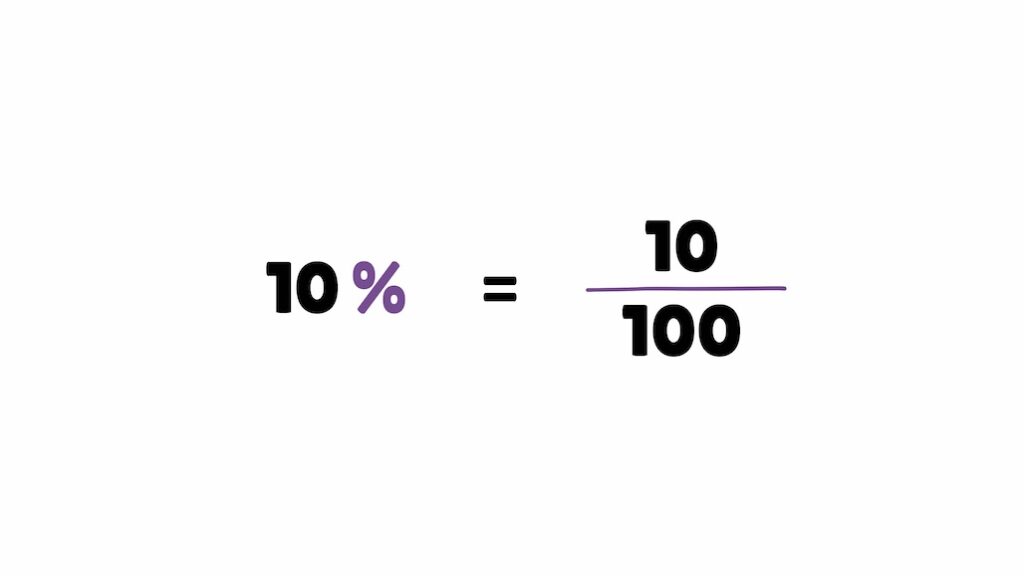
And if you ever forget how percentages work, flip the symbol back sideways. 10% is 10 over 100, which is point 1.
Sources
- Percent sign – Wikipedia.org
Dig deeper!
- Learn how to convert between percentages and decimals with IXL’s interactive exercises.
- Read this excerpt from GCF Global to better understand how to convert fractions, decimals and percentages.
- Practice your skills with more free exercises from Mathisfun.
Classroom activity
Objective:
Students will develop a conceptual understanding of percentages by relating them to fractions and decimals through visual models, real-life examples, and guided problem-solving.
Materials Needed:
- Access to the Sprouts video on percentages
- Whiteboard of flip chart
- Markers
- Paper or digital devices for student notes
- Printable hotel room scenario cards (optional)
Duration:
60 minutes
Steps:
1. Introduction (4 minutes)
- Start with: “If you had to increase your pocket money by 10% or shrink your screen time by 40%, could you do the math in your head?”
- Let students give guesses
2. Give it a try (8 minutes)
- Students get together in pairs and try to solve 2 questions on a sheet of paper. , For example: if you want to earn 10% more in your current job, how much more do you need to ask for?
3. Play the Sprouts video (4 minutes)
4. Concept Mapping in Pairs (10 minutes)
Students pair up to create a quick concept map:
- What is a percent?
- How does it connect to fractions and decimals?
- How can it be used to increase or decrease values?
5. Hotel Math Challenge (14 minutes)
- In small groups, students act as hotel managers using provided scenarios (e.g., “increase capacity by 25%”, “reduce rooms by 40%”).
- They calculate using decimals and multipliers and explain the logic behind their answer.
6. Whole-Class Concept Discussion (15 minutes)
- Groups share their reasoning. The teacher guides the discussion, highlighting the shift from “percent” to “decimal” to “multiplier”.
- The teacher demonstrates how the % symbol is like a fraction. Students sketch or write what 25%, 50%, 100% would look like as part/whole models.
7. Reflection and Sharing (5 minutes)
- Students each write a real-life situation where they’ve encountered percentages and how they would now approach it using this concept.
- Invite a few students to share. Wrap up with: “What changed in how you understand percentages today?”
Collaborators
- Script: Jonas Koblin
- Cartoon artist: Pascal Gaggelli
- Producer: Selina Bador
- Voice artist: Matt Abbott
- Coloring: Nalin
- Editing: Peera Lertsukittipongsa
- Publishing: Vijyada Songrienchai

